[생각보다 쉬운 통계학] 3.분포 - 연속형 분포 (2)
😀 이번 포스팅의 목표는 아래 분포를 살펴보려고 합니다.
1. 와이블분포
2. 정규분포 및 표준정규분포
3. 중심극한정리
지난 포스팅에서 균일분포, 감마분포, 지수분포, 베타분포에 대해서 살펴보았습니다.
이번 포스팅에서는 와이블분포와 정규분포, 그리고 중심극한정리에 대해 살펴보겠습니다.

연속형 분포는 주황색 박스입니다.
5. 와이블분포(Weibull distribution)
- 와이블 분포(Weibull distribution)
고장률함수의 분포에 따라 고장 확률 밀도 함수를 표현하는 확률분포
🤔 고장률함수가 무엇인지 들어보지 못했죠,, - 신뢰도 함수(Reliability function)
특정 시간까지 '고장' 없이 주어진 임무를 수행할 확률
확률변수 $X$를 수명일 때, $ R(x) = 1-F(x) $
여기서 $F(x)$는 와이블분포의 누적분포함수입니다. - 고장률 함수(Hazard rate function)
확률변수 $X$를 수명일 때,
수명까지 '고장'없이 주어진 임무를 수행하다가 수명 직후 '고장'이 발생할 단위 시간당 빈도의 확률
$ \lambda(x) = \cfrac{f(x)}{R(x)} = \left( \cfrac{ \lambda }{\sigma} \right) \left( \cfrac{x}{\sigma} \right)^{ \lambda - 1} $
여기서 $f(x)$는 와이블분포의 확률밀도함수입니다.
> 와이블분포 확률밀도함수
$$ X \sim Wei(\sigma , \lambda) $$
$$ f(x; \mu , \sigma , \lambda) = \cfrac{\lambda}{\sigma^{\lambda}} \left( x - \mu \right)^{\lambda - 1} exp \left[ - \left( \cfrac{x - \mu}{\sigma} \right )^{\lambda} \right ], \;\;\, x>0, \sigma > 0, \lambda >0, - \infty < \mu < \infty $$
여기서 $x$는 사건이 발생할 때까지의 대기시간, 즉 수명입니다.
또한, $\mu$는 위치 모수, $\sigma$는 척도 모수, $\lambda$는 형태 모수입니다.
척도 모수는 $x$의 측정 단위 크기를 반영하고, 형태 모수에 따라 분포의 모양이 결정됩니다.
형태모수에 관해서는 아래 특징에서 더 설명하겠습니다.
> 와이블분포 누적분포함수
$$ F(x, \sigma, \lambda) = 1 - exp \left[ - \left ( \cfrac{x - \mu}{\sigma} \right )^{\lambda} \right ] $$
> 확률분포함수 조건
- $ \cfrac{\lambda}{\sigma^{\lambda}} \left( x - \mu \right)^{\lambda - 1} exp \left[ - \left( \cfrac{x - \mu}{\sigma} \right )^{\lambda} \right ]> 0 $
- $ \int_{R}^{} \cfrac{\lambda}{\sigma^{\lambda}} \left( x - \mu \right)^{\lambda - 1} exp \left[ - \left( \cfrac{x - \mu}{\sigma} \right )^{\lambda} \right ]dx = 1 $
> 확률분포함수 특징
- 생존분석과 신뢰성 분석 분야에서 사용됨
- $\lambda$의 값이 3.26에 근사할수록 최빈값과 중앙값 동일
- $ 3 < \lambda < 4 $인 경우 분포 모양은 대칭 형태
- 형태 모수의 값에 따른 다른 분포 간 관계
- $ \lambda < 1$ : 감마분포
- $ \lambda = 1$ : 지수분포 Exp(1)
- $ \lambda = 2$ : 레일리히분포
- $ \lambda = 3.5$ : 정규분포 근사
> 평균(기댓값), 분산, 표준편차
- 평균(기댓값) 유도
여기서 유도된 기댓값은 평균 고장시간을 의미합니다.
\begin{align}
E(X) &= \int_{0}^{\infty} x \times \cfrac{\lambda}{\sigma^{\lambda}} x^{\lambda - 1} exp \left[ - \left( \frac{x}{\sigma}^{\lambda} \right ) \right ] dx \\
& Let, y = \left( \frac{x}{\sigma} \right )^{\lambda} \\
& \int_{0}^{\infty} \lambda y^{\frac{1}{\lambda}} e^{-y} dy \\
&= \sigma \int_{0}^{\infty} y^{\frac{1}{\lambda}} e^{-y} dy \\
&= \sigma \Gamma(1+\frac{1}{\lambda})
\end{align} - 분산 유도
$ Var(x) = E(X^2) - \left[ E(X) \right ]^2$의 과정으로 유도하겠습니다.
\begin{align}
E(X^2) &= \int_{0}^{\infty} x^{2} \times \frac{\lambda}{\sigma^{\lambda}} exp \left[ - \left( \frac{x}{\sigma} \right)^{\lambda} \right ] dx \\
& Let, y = \left( \frac{x}{\sigma} \right )^{\lambda} \\
&= \int_{0}^{\infty} \left( \lambda y^{\frac{1}{\lambda}} \right)^2 e^{-y} \\
&= \sigma^2 \int_{0}^{\infty} y^{\frac{2}{\lambda}} e^{-y} dy \\
&= \sigma^2 \Gamma \left( 1+\frac{2}{\lambda} \right)
\end{align}
\begin{align}
Var(X) &= E(X^2) - \left[ E(X) \right ]^2 \\
&= \sigma \Gamma \left(1 + \frac{2}{\lambda} \right) - \left[ \sigma \Gamma \left( 1+ \frac{1}{\lambda} \right ) \right ]^2 \\
&= \sigma^2 \left\{ \Gamma \left(1+ \frac{2}{\lambda} \right ) - \left[ \Gamma \left( 1+ \frac{1}{\lambda} \right) \right ]^2 \right \}
\end{align} - 표준편차
$$ \sqrt{ \sigma^2 \left\{ \Gamma \left(1+ \frac{2}{\lambda} \right) - \left[ \Gamma \left( 1+ \frac{1}{\lambda} \right ) \right]^2 \right\} } $$
> 그래프
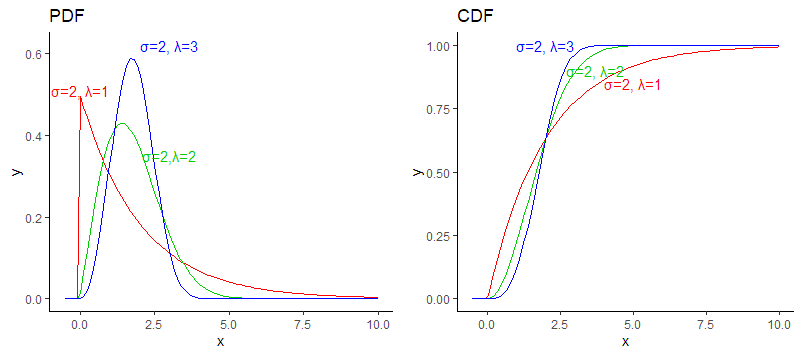
코드
#pdf
g1 <- ggplot(data.frame(x=seq(-0.5,10,0.1)), aes(x=x)) +
stat_function(fun=dweibull, args=list(scale=2, shape=1), col="red")+
stat_function(fun=dweibull, args=list(scale=2, shape=2), col="green3")+
stat_function(fun=dweibull, args=list(scale=2, shape=3), col="blue")+
labs(title="PDF") +
theme_classic()+
annotate("text", x=0, y=0.51, label="σ=2, λ=1", col="red") +
annotate("text", x=3, y=0.35, label="σ=2,λ=2", col="green3") +
annotate("text", x=3, y=0.62, label="σ=2, λ=3", col="blue")
#cdf
g2 <- ggplot(data.frame(x=seq(-0.5,10,0.1)), aes(x=x)) +
stat_function(fun=pweibull, args=list(scale=2, shape=1), col="red")+
stat_function(fun=pweibull, args=list(scale=2, shape=2), col="green3")+
stat_function(fun=pweibull, args=list(scale=2, shape=3), col="blue")+
labs(title="CDF") +
theme_classic()+
annotate("text", x=5, y=0.85, label="σ=2, λ=1", col="red") +
annotate("text", x=3.7, y=0.9, label="σ=2, λ=2", col="green3") +
annotate("text", x=2, y=1, label="σ=2, λ=3", col="blue")
grid.arrange(g1, g2, ncol=2)
6. 정규분포(Normal distribution)
사실 기초 통계에서 가장 중요하고, 많이 사용되는 분포입니다.
- 정규 분포(Normal distribution)
기댓값을 중심으로 중심위치는 기댓값, 산포는 표준편차에 의해 결정되는 분포
> 정규분포 확률밀도함수
$$ X \sim N( \mu , \sigma^2 ) $$
$$ f(x; \mu, \sigma) = \cfrac{1}{\sqrt{2 \pi} \sigma} exp \left[ - \cfrac{(x- \mu)^2}{2 \sigma^2} \right ], \;\;\, -\infty <x<\infty, -\infty <\mu<\infty, 0<\sigma<\infty $$
여기서 $\mu$는 $E(X)$, $\sigma^2$는 $Var(X)$입니다.
> 확률분포함수 조건
- $ \cfrac{1}{\sqrt{2 \pi} \sigma} exp \left[ - \cfrac{(x- \mu)^2}{2 \sigma^2} \right ] > 0 $
- $ \int_{-\infty}^{\infty} \cfrac{1}{\sqrt{2 \pi} \sigma} exp \left[ - \cfrac{(x- \mu)^2}{2 \sigma^2} \right ] dx = 1 $
> 확률분포함수 특징
- 불확실성

구간 $(\mu - \sigma, \mu + \sigma)$의 확률은 68%,
구간 $(\mu - 2\sigma, \mu + 2\sigma)$의 확률은 95%,
구간 $(\mu - 3\sigma, \mu + 3\sigma)$의 확률은 99.7%입니다.
여기서 $\pm k \sigma$를 불확실성으로 일컫습니다.
위 그래프의 코드가 궁금하다면?!
x1 <- seq(-10,10,0.01); y1 <- dnorm(x1,0,1)
plot(x1,y1,type="l",xaxt="n",yaxt="n",xlim=c(-6,6),lwd=2,col="lightblue", ylab="")
x <- c(-6:6); y <- dnorm(x,0,1)
segments(x[4],0,x[4],y[4], col="gray", lty="dotted"); axis(side=1, at=-3, labels="μ-3σ")
segments(x[5],0,x[5],y[5], col="gray", lty="dotted"); axis(side=1, at=-2, labels="μ-2σ")
segments(x[6],0,x[6],y[6], col="gray", lty="dotted"); axis(side=1, at=-1, labels="μ-1σ")
segments(x[7],0,x[7],y[7], col="gray", lty="dotted"); axis(side=1, at=0, labels="μ")
segments(x[8],0,x[8],y[8], col="gray", lty="dotted"); axis(side=1, at=1, labels="μ+1σ")
segments(x[9],0,x[9],y[9], col="gray", lty="dotted"); axis(side=1, at=2, labels="μ+2σ")
segments(x[10],0,x[10],y[10], col="gray", lty="dotted"); axis(side=1, at=3, labels="μ+3σ")
segments(x[4],y[4]+0.00005,x[10],y[10]+0.00005, col="black", lty="solid");rect(-.5,0,.5,.005,col="white",border=NA); text(0,0.0045,labels="99.73%")
segments(x[5],y[5]+0.00005,x[9],y[9]+0.00005, col="black", lty="solid");rect(-.5,.03,.5,.065,col="white",border=NA); text(0,0.054,labels="95.45%")
segments(x[6],y[6]+0.00005,x[8],y[8]+0.00005, col="black", lty="solid");rect(-.5,0.2,.5,.3,col="white",border=NA); text(0,0.242,labels="68.27%")
- 선형변환
- $X \sim N(\mu, \sigma^2)$일 때, $Y = a+bX$라고 한다면,
$Y \sim N(a+b \mu, b^2 \sigma^2) $
- $X \sim N(\mu, \sigma^2)$일 때, $Y = a+bX$라고 한다면,
- 가법성
- $ X \sim N(\mu_{1}, \sigma_{1}^{2}), Y \sim N(\mu_{2}, \sigma_{2}^{2})$이고, $X$와 $Y$가 독립이라면,
$ X + Y \sim N(\mu_{1} + \mu_{2}, \sigma_{1}^{2} + \sigma{2}^{2} $ - 만약, $X$와 $Y$가 독립이 아니라면,
$ X + Y \sim N(\mu_{1} + \mu_{2}, \sigma_{1}^{2} + \sigma{2}^{2} + 2 \sigma_{XY} $ - 조금 더 일반화해서 적어보면,
$X_{i} \sim N( \mu_{i}, \sigma_{i}^{2}), i = 1,2,\cdots, n$으로 각 $X$가 독립적으로 정규분포를 따른다면,
$Y = \sum_{i=1}^{n} X_{i}$일 때, $ Y \sim N(\sum_{i=1}^{n} \mu_{i}, \sum_{i=1}^{n} \sigma_{i})$
- $ X \sim N(\mu_{1}, \sigma_{1}^{2}), Y \sim N(\mu_{2}, \sigma_{2}^{2})$이고, $X$와 $Y$가 독립이라면,
- 이항분포의 정규 근사
- 이항분포에 대한 설명은 https://begin-stat.tistory.com/8 을 참고해주세요.
- $ X \sim B(n,p)$이면, $ Z = \frac{X-np}{\sqrt{np(1-p)}} \sim N(0,1) $
이항분포를 따르는 확률변수에 대해서 $np$와 $np(1-p)$, 즉 기댓값과 분산이 모두 15보다 클 때,
평균 $np$, 표준편차 $ \sqrt{np(1-p)}$인 정규분포에 의해 근사됩니다.
- 중심극한정리(Central limit theorem, CLT)
- 모집단의 분포가 어떠한 분포를 따르는 것에 관계없이 $n$이 크면 표본 평균 $E \overline{X} $는 근사적으로 정규분포를 따릅니다.

임의의 이항분포에서 표본을 추출한 히스토그램과 정규 곡선을 나타낸 그림입니다.
$n$의 값이 증가할수록 정규 곡선에 유사한 것을 확인할 수 있습니다.
http://www.ltcconline.net/greenl/java/Statistics/clt/cltsimulation.html 에서
클릭으로 모의실험 해볼 수 있다고 하네요.
위 그래프의 코드가 궁금하다면?!
m = c()
num = c(30, 50, 100,200)
for(n in num){
for(i in 1:n){
m[i] = mean(rbinom(30, size=n, prob=.5))
}
hist(scale(m), prob=T, col='lightgray')
curve(dnorm(x, 0, 1), -3, 3, col='blue', add=T)
}
> 평균(기댓값), 분산, 표준편차
- 평균(기댓값) 유도
\begin{align*}
E(X) &= \int_{-\infty}^{\infty} x \times \frac{1}{\sqrt{2 \pi} \sigma} exp \left[ - \frac{(x-\mu)^2}{2 \sigma^{2}} \right] dx \\
&= \frac{1}{\sqrt{2 \pi}\sigma} \int_{- \infty}^{\infty} (x- \mu + \mu) \times exp \left[ - \frac{(x- \mu)^2}{2 \sigma^2} \right] dx \\
&= \frac{1}{\sqrt{2 \pi} \sigma} \left \{ \int_{- \infty}^{\infty} (x- \mu) \times exp \left [ - \frac{(x- \mu)^2}{2 \sigma^2} \right ] dx + \int_{- \infty}^{\infty} \mu \times exp \left[ - \frac{(x-\mu)^2}{2 \sigma^2} \right ] dx \right \} \\
&= \frac{1}{\sqrt{2 \pi} \sigma} \int_{-\infty}^{\infty} \mu \times \left[ - \frac{(x-\mu)^2}{2 \sigma^2} \right ] dx \\
&= \mu \int_{- \infty}^{\infty} \frac{1}{\sqrt{2 \pi} \sigma} exp \left[ - \frac{(x-\mu)^2}{2 \sigma^2} \right ] dx \\
&= \mu
\end{align*} - 분산 유도
$ E(X^2) - \left ( E(X) \right )^2 $으로 계산하겠습니다.
상당히 길어 한글에서 수식 캡처 하였으며, 일부 과정은 생략했습니다.


- 표준편차
$$ \sqrt{ \sigma^2 } = \sigma $$
> 그래프
평균 2, 분산 25인 그래프입니다.

위 그래프의 코드가 궁금하다면?!
par(mfrow=c(1,2))
x <- -300:300/15
plot(x, dnorm(x, mean=2, sd=5), type="l", main="PDF", lwd=2,col="royalblue")
plot(x, pnorm(x, mean=2, sd=5), type="l", main="CDF", lwd=2,col="royalblue")
7. 표준정규분포(Standard normal distribution)
- 표준 정규 분포(Standard normal distribution)
기댓값 0, 표준편차 1인 정규분포
$ X \sim N(\mu, \sigma^2)$일 때, $Z = \frac{X - \mu}{\sigma}$이면, $Z \sim N(0,1)$
: 정규분포를 따르는 확률변수를 표준화하면, 표준정규분포를 따릅니다.
> 표준정규분포 확률밀도함수
$$ X \sim N( 0, 1 ) $$
$$ \phi(z) = \cfrac{1}{\sqrt{2 \pi}} exp \left( - \cfrac{z^2}{2} \right ), \;\;\, -\infty <z<\infty $$
> 확률분포함수 조건
- $ \cfrac{1}{\sqrt{2 \pi}} exp \left( - \cfrac{z^2}{2} \right ) > 0 $
- $ \int_{-\infty}^{\infty} \cfrac{1}{\sqrt{2 \pi}} exp \left( - \cfrac{z^2}{2} \right ) dx = 1 $
> 확률분포함수 특징
- $ \phi(\infty) = 1, \phi( -\infty) = 0 $
- $\phi(0) = 0.5$
- $\phi(-x) = 1-\phi(x)$
> 평균(기댓값), 분산, 표준편차
- 평균(기댓값) 유도
\begin{align*}
E(X) &= \int_{- \infty}^{\infty} x \frac{1}{\sqrt{2 \pi}} exp \left( - \frac{1}{2} x^2 \right ) dx \\
&= \frac{1}{\sqrt{2 \pi}} \int_{- \infty}^{0} x \times exp \left( - \frac{1}{2} x^2 \right ) dx + \frac{1}{\sqrt{2 \pi}} \int_{0}^{\infty} x \times exp \left( - \frac{1}{2} x^2 \right ) dx \\
&= \frac{1}{\sqrt{2 \pi}} \left[ - exp \left ( - frac{1}{2} x^2 \right) \right]_{-\infty}^{0} + \frac{1}{\sqrt{2 \pi}} \left[ - exp \left ( - frac{1}{2} x^2 \right) \right]_{0}^{\infty}\\
&= \frac{1}{\sqrt{2 \pi}} \left[ -1 + 0 \right] + \frac{1}{\sqrt{2 \pi}} \left[ 0 + 1 \right]\\
&= - \frac{1}{\sqrt{2 \pi}} + \frac{1}{\sqrt{2 \pi}} \\
&= 0
\end{align*} - 분산 유도
$ E(X^2) - \left ( E(X) \right )^2 $으로 계산하겠습니다.
\begin{align*}
E(X^2) &= \int_{- \infty}^{\infty} x^2 \frac{1}{\sqrt{2 \pi}} exp \left( - \frac{1}{2} x^2 \right ) dx \\
&= \frac{1}{\sqrt{2 \pi}} \left \{ \int_{-\infty}^{0} x \left (x \times exp \left( - \frac{1}{2} x^2 \right ) \right ) dx + \int_{0}^{\infty} x \left ( x \times exp \left( - \frac{1}{2} x^2 \right ) \right ) dx \right \} \\
&= \frac{1}{\sqrt{2 \pi}} \left \{\left[-x \times exp \left ( - \frac{1}{2} x^2 \right ) \right]_{- \infty}^{0} + \int_{- \infty}^{0} exp \left ( - \frac{1}{2} x^2 \right ) dx + \left[-x \times exp\left ( - \frac{1}{2} x^2 \right ) \right]_{0}^{\infty} + \int_{0}^{\infty} exp \left( - \frac{1}{2} x^2 \right ) dx \right \} \\
&= \frac{1}{\sqrt{2 \pi}} \left \{(0-0)+(0-0)+ \int_{-\infty}^{0} exp \left( - \frac{1}{2}x^2 \right) dx + \int_{0}^{\infty} exp \left( - \frac{1}{2} x^2 \right ) dx \right \} \\
&= \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} exp \left( - \frac{1}{2} x^2 \right) dx \\
&= 1
\end{align*}
\begin{align*}
Var(X) &= E(X^2) - \left ( E(X) \right )^2 \\
&= 1 - 0^2 \\
&= 1
\end{align*}
- 표준편차
$$ \sqrt{ 1 } = 1 $$
> 그래프

위 그래프의 코드가 궁금하다면?!
par(mfrow=c(1,2))
x <- -300:300/15
plot(x, dnorm(x, mean=0, sd=1), type="l", main="PDF", lwd=2,col="royalblue")
plot(x, pnorm(x, mean=0, sd=1), type="l", main="CDF",lwd=2,col="royalblue")
저번 포스팅에 미처 넣지 못했던 와이블분포, 그리고 정규분포에 대해 살펴보았습니다.
정규분포와 중심극한정리에 대해 꼭 기억해주시고,
다음 포스팅부터는 정규분포로부터 유도할 수 있는 분포를 추가로 더 알아보며 마치겠습니다😊
'생각보다 쉬운 통계학 > 수리통계학' 카테고리의 다른 글
| [생각보다 쉬운 통계학] 3.분포 - 연속형 분포 (3) (0) | 2022.02.22 |
|---|---|
| [생각보다 쉬운 통계학] 3.분포 - 연속형 분포 (1) (0) | 2022.01.26 |
| [생각보다 쉬운 통계학] 3.분포 - 이산형 분포 (2) (0) | 2022.01.16 |
| [생각보다 쉬운 통계학] 3. 분포 - 이산형 분포 (1) (0) | 2022.01.10 |
| [생각보다 쉬운 통계학] 2. 분포 관련 개념 정의 (2) (0) | 2022.01.01 |

